Efficency of the Generation

To consider the efficiency of our hydroelectricity generation system we must consider the following equation P_net = e₀gpqh_gross ⁸ where e₀ is the characteristic overall efficiency of our system, g is the gravitational constant which we will take as 9.81, h_gross is the gross head which is the height water will fall in our system which we may or may not b e able to control, p is the density of water which we will approximate to 1000kg/m³ and q is water flow in m³/s which we will be able to vary dependant on the total water that will be available to us at the given location and the current electricity needs. P_net is the net power produced. When installing our generator it will also be useful to consider our plant factor which is given as power output over the potential maximum power output, the potential max power would be given by the generator running at full capacity with a corresponding level of water flow and the expected power output would mainly be limited by the reality of the water flow in the location we choose. In our power equation, given above, e₀ is not an imperially known variable. This is the case because our efficiency will be based on a number of factor such as: the efficiency of the generator we choose to use, considerations of friction effecting our gross head calculation and the efficiency of the turbine/water wheel we choose to use. Calculating efficiency without experimental data and precise information on equipment being used is very imprecise and as a future step prototyping to refine the value of the variable used in our calculations. For this project we have chosen to use a turbine for our generation. This is because research suggest that for the sort of gross head we are likely to have available a turbine will be much more efficient than the alternative option of using a water wheel with potential efficiencies for turbines standing at 75-80% ⁸ this is because we are generating on a small scale and are likely to be using small falls of water in the range of 5-15 ft. for our generation, water wheels are much more inefficient at small falls, the smallest fall that could potentially generate a reasonable amount of power is 2 ft. 6 in, but the efficiency would fall by 5-10%.

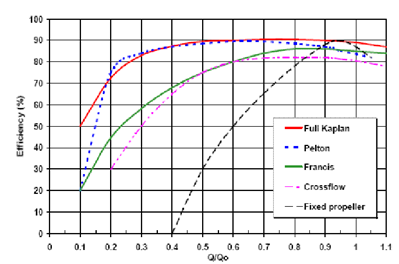
To go even deeper we can compare various types of water turbine and select a design that best fits our requirements. Observing the graph below⁷ Kaplan and Pelton types are most efficent at the low water speeds we can expect, however the Pelton design is most appropraite for use in a small machine. To harness the maximum power output, the Pelton wheel needs to run at half the speed of water jet entering the turbine. The water will leave the wheel at very slow speed, enabling the system to extract most of its energy making it very efficient.

For large scale transmission it is efficient to use step up and step down transformers to ensure minimal power losses in transmission by having the electricity transmitted over long distances at a very high voltage, as P = V²/R which is then stepped down to a useable level nearer the consumer. However considering that we are planning to generate power very locally to where it is being consumed and the need to keep costs and complexity low we will generate, transmit and use electricity at consistent voltage of 230v. It is hard to state the exact losses in the cables without knowing the length of the cables and the resistance of the material they will be made of, however losses in transmission cables are anticipated to be low due to the short length of our transmission cables.