
Note: Some of the graphical elements of this site are only visible to browsers that support accepted web standards. The content of this site is, however, accessible to any browser or Internet device.
Control and Power Portfolio Partnership
Robust Model Predictive Control
Research Activities
Model predictive control takes direct account of constraints on control and output variables, it is easy to implement even for nonlinear systems and theory giving a precise description of systems for which model predictive strategies are stabilizing is available. However, these advantages are off-set by the need for extensive on-line calculations, a lack of detailed information about closed loop transient response and performance degradation due to modelling errors and disturbances.
Current research is therefore focused on techniques for reducing sensitivity of closed loop response to modelling errors and disturbances (improved robustness). Another direction of current research is improvement of existing computational methods and of course reduction of computational demands.
Tubes & Robust Model Predictive Control
Recent MPC schemes ensure convergence of state trajectories to a pre-specified desired region, for systems with additive but bounded disturbances. Control action is applied so that the closed loop state trajectory remains within a minimal tube around a nominal path whatever the disturbance. The following figure illustrate the improvement achieved by robust MPC as compared with standard schemes.
Linear System with additive disturbance


RMPC versus open loop control RMPC versus conventional MPC
The red boxes contain the spread of the trajectories for different disturbances. The diagram illustrate that Robust MPC maintains state trajectories in the 'tube', regardless of disturbances. Standard MPC fails to do so.
Linear parametrically uncertain system
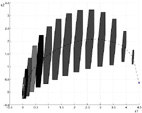

Optimal Tube A set of sample trajectories
The optimal 'tube' contain the spread of the trajectories for different parameter realizations. The diagram illustrate that the 'tube' maintains state trajectories in the 'tube' for all possible parameter variations.
Piecewise affine systems (with 2 partitions) with additive disturbance

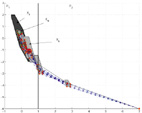
Optimal Tube with robust switching Optimal Tube with robust switching
The optimal 'tube' contain the spread of the trajectories for all disturbances and moreover it ensures the robust switching of piecewise affine system.
Explicit Receding Horizon Control
The burden of on-line computations is a shortcoming of some of traditional implementations of MPC. Recent advances, made by a number of contributors (Pistikopoulos, Dua, Goodwin, Seron, Bemporad, Morari, Borreli, Kerrigan, Mayne, Rakovic, Tondel, Johansen and others), permit a large part of these computations to be carried out off-line, prior to implementation, in certain important cases. The computational burden of implementing the MPC scheme is correspondingly considerably reduced.
If the system is linear/affine or piecewise affine and the cost linear or quadratic, the state space may be decomposed into a collection of polytopic cells, in each of which an affine control law is operative. Efficient methods are now available for pre-computing the cells and the associated optimal control laws. The following figures illustrate the regions of constant 'optimal' gain for a range of the examples, with different types of constraints
Explicit RHC, LTI system & quadratic cost
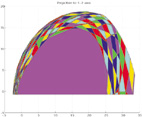

LTI System, control and state constraints and horizon = 10 time periods
Explicit RHC, PWA system & quadratic cost
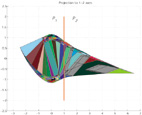
PWA System 2 partitions, control and state constraints and horizon = 7 time periods