Antimatter Propulsion
Introduction
In this section of the report, we will be looking into antimatter propulsion—a highly advanced technology of the future. Antimatter was first predicted by a Cambridge physicist named Paul A.M. Dirac who combined Schrodinger’s equation of quantum mechanics and Einstein’s theory of special relativity which predicted the existence of 4 different kinds of electrons, i.e. spin up or down with positive or negative energy. In a symmetrical sense, these electrons with negative energy have negative mass and a negative charge (antimatter) which is equivalent but opposite to its counterpart with positive energy. The reality of antimatter was confirmed by Carl Anderson, who in 1932 discovered positrons (or anti-electrons) in cosmic ray induced events. Subsequently, the existence of anti matter has been proven multiple times with the production of an anti-proton at Berkeley Bevatron in 1955 and anti-atoms at CERN.
The collision between a proton and an anti-proton will result in an explosion emitting pure radiation which travels out at the speed of light. Based on Einstein’s equation as previously mentioned, the energy produced will be their combined mass in energy and the 2 particles will be totally annihilated. Put in more practical terms, this means that a gram of antimatter is capable of producing the total energy equivalent to almost 2 dozen Space Shuttle external fuel tanks. As such, antimatter could be an ideal fuel source for space propulsion.
In the next section, we will look into 3 different technologies which use antimatter for propulsion.
Hybrid Antimatter-Nuclear Drives
Given the current production capacity of antimatter (nanograms per year) and storage facilities, it is not possible to produce sufficient quantities to fuel a spacecraft purely with antimatter. The current drive concepts being tested are hybrid antimatter-nuclear drives, where the antimatter is only used to catalyse or initiate nuclear drives. There are 2 implementations of this concept, the first of which is the Antimatter Catalysed Micro Fission/Fusion (ACMF) Drive being developed at The Pennsylvania State University.
Antimatter Catalysed Micro Fission/Fusion Drive
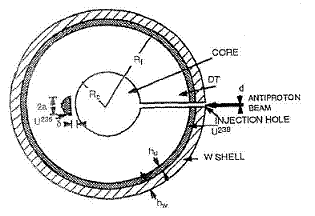
Pellet geometry
ACMF Drive utilises antimatter to kick start a fission reaction which subsequently induces a fusion reaction. The beauty of this concept is that it reduces difficulties associated with each of the individual stages. Antimatter is only required in small quantities; a maximum of 100 g for intra-system travel up to Pluto. In addition, minimal fission is required to start the fusion reaction which reduces radioactive waste, and fusion which is difficult to sustain only has to be maintained for a short time. The propellant will come in the form of a pellet of deuterium, tritium and uranium-238 (9 parts D-T to 1 part U-238). It is firstly injected into a reaction chamber where it will undergo compression by ion particle beams. Subsequently, the propellant will be irradiated with a burst of antiprotons. The antiprotons will annihilate some of the pellet, releasing sufficient energy to initiate fission of U-238. Following which, the fission reaction causes fusion to commence in the D-T core. The products of the entire process are in the form of radiation and hot plasma which is ejected to produce the thrust for the spacecraft.
Antimatter Initiated Microfusion Drive
Diagrammatic demonstration of AIM Drive
AIM Drive is similar to the ACMF Drive in that it uses antiprotons to ignite a fission reaction and subsequently a fusion reaction. However the method is significantly different and it will produce more power overall, requiring more antimatter in the process.
With this method, the D-T fuel droplet is mixed with a small concentration of lead-208 or uranium-238 and injected into a plasma cloud of antiprotons. The antiprotons are held in a special Penning trap as charged plasma which is compressed using electric and magnetic fields creating a potential well. Like ACMF, U-238 undergoes rapid fission when it collides with the antiprotons. The fission reaction fully ionises the deuterium/helium-3 fuel into plasma which undergoes nuclear fusion and is compressed by the potential well of antiprotons. The charged particles formed as the product of the fusion will be expelled either through a magnetic nozzle or transferred to a propellant such as hydrogen to produce thrust. This reaction can occur 50 times before the trap has to be reloaded.
Antimatter Driven Sail
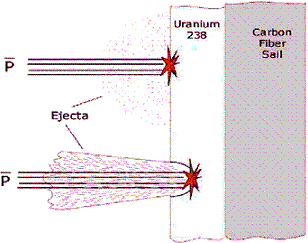
Antimatter colliding with sail
This technology is developed based on our limitations on antimatter production. Only a producible amount of antimatter is required to produce the thrust. This technology uses nuclear fission to produce the thrust onto a sail which will accelerate the rocket through space. The sail is composed of 2 layers: a carbon backing (sail) and a uranium-238 coating (fuel). For fission to occur, antimatter will be released towards the sail. Upon coming into contact with the uranium foil, a fission event will be induced. This will produce 2 main fragments with a velocity of 1.39×107 m/s which equates to a specific impulse of 1.4 million seconds. In practice, not all the momentum will be transferred to the sail and generally, half of the fission particles will be ejected away from the foil. It has been theorised that annihilation beneath the surface of the sail will create a cloud of ejecta which will boost the momentum transferred to the sail, making the fission reaction more efficient. This can be done by accelerating the incident antiprotons towards the sail by electrostatically biasing the sail and the antimatter container. Potentially, this gives us a way of controlling the specific impulse we need by controlling the energy of the incident antimatter beam onto the sail.
Theoretical Beam-Core Antimatter Propulsion System
The previous few methods discussed are based on nuclear reactions generating the thrust for the rocket and antimatter is only required in smaller quantities in relation to the fuel. However, the tremendous energy generated in matter and antimatter annihilation cannot be fully exploited. We will now look at a theoretical propulsion system that will fully utilise antimatter as fuel to produce the thrust.
The idea is to simply eject the products of the annihilation out of the rocket to produce the propulsion force. This method will generate 300 times more energy than any nuclear fusion reaction. Annihilation of protons and antiprotons occur in a magnetic nozzle producing uncharged and charged pions. Guided by the magnetic field, charged pions travel down the magnetic nozzle at close to the speed of light before decaying into electrons and positrons. As the charged and uncharged particles possess mass, the reaction is not 100% efficient. However, 64% efficiency (5.8×1016 J/kg) can be obtained.
The uncharged pions are unaffected by the magnetic field and decay into gamma rays that are not directed down the nozzle. If the gamma rays can be directed or reflected, this will greatly increase the efficiency factor. Eugen Sänger proposed a theory that an extremely dense electron gas can act as a reflector to channel the gamma rays into a well-collimated exhaust beam. Giovanni Vulpetti has also proposed that by interacting the rays with the electric field of a nucleus, real electron-positron pairs can be formed. The now charged particles can be collimated by the magnetic field and directed down the nozzle. In either case, even if half of the gamma rays are utilised, we are still able to obtain a specific impulse of approximately 0.77c.
Conclusion
This futuristic technology has given us a glimpse into the future of space travel. Compared to current conventional rocket fuels, the biggest advantage of antimatter propulsion is the much higher specific impulse which allows travel out of our interplanetary system and even beyond Alpha Centauri. Furthermore, it is the most energy dense substance known to man, and this means that we need to carry much less fuel in terms of weight as compared to chemical rockets. However, many technological barriers have to be overcome before an antimatter rocket can be created. The main hurdles are the production and storage of large amounts of antimatter. Today, the cost of producing 1 gram of antimatter is $25 billion, and the rate of production is only at 10 nanograms (maximum) per year. Current technology only allows us to store small amounts of antimatter in each Penning trap. However ongoing research to increase production and storage capacities could lead to a breakthrough.
Bibliography
- "The Physics of Starship Design." 28 Dec 2009 <http://ffden-2.phys.uaf.edu/213.web.stuff/scott%20kircher/>.
- "Fusion Reactions And Matter-Antimatter Annihilation For Space". Bât. 210, UPS, 91405 Orsay, France : LPGP (UMR-CNRS 8578), 13 JUL 2005.
- G. Gaidos, R.A. Lewis and G.A. Smith, B. Dundore, S. Chakrabarti. "Antiproton-catalyzed Microfission/fusion Propulsion Systems For Exploration": The Pennsylvania State University.
- Meyer, Kirby J. 26 Dec 2009 <http://www.engr.psu.edu/antimatter/introduction2.html>.
- Raymond A. Lewis, Kirby Meyer, Gerald A. Smith, Steven D. Howe. "AIMStar: Antimatter Initiated Microfusion For Pre-cursor Interstellar Missions" The Pennsylvania State University.
- McMahon, Patrick B. "Antimatter Initiated Microfission/fusion (AIM) Space Propulsion". 2000.
- Gilster, Paul. "Antimatter Propulsion: A Critical Look" 29 Dec, 2009. <http://www.centauri-dreams.org/?p=8081>
- Dr.Steven D. Howe, Dr. Gerald P. Jackson. "NIAC Phase I Progress Report Antimatter Driven Sail for Deep Space Missions". NIAC.
- Gerald P. Jackson, Steven D. Howe. "Antimatter Driven Sail For Deep Space Mission". 2003 Particle Accelerator Conference.
- "Antimatter: Beam Drive". 3 Jan 2010 <http://ffden-2.phys.uaf.edu/213.web.stuff/scott%20kircher/beamedcore.html>
- Frisbee, Robert H. "How to build an antimatter rocket for interstellar missions". Huntsville, Alabama : 39th AIAA/ASME/SAE/SAEE Joint Propulsion Conference and Exhibit, 2003. AIAA 2003-4676.
- Westmoreland, Shawn. "A note on Relativistic Rocketry. Manhattan, Kansas : Department of Mathematics", Kansas State University, 2009, October 13.
- Wikipedia contributors. "Antimatter." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 3 Jan 2010 <http://en.wikipedia.org/wiki/Antimatter>





